A többdimenziós skálázást (MDS) egy dimenziócsökkentő eljárás, melyet először a földrajzban használtak térképek kirajzolására. Azóta számos más területen is alkalmazzák, pl. pszichológiában kognitív térképek. Ennek a bejegyzésnek a célja az MDS alkalmazásának bemutatása R-ben. Példaként Magyarország térképét fogjuk kirajzolni települések távolságmátrixának felhasználásával.
Hazánk távolságmátrixát a http://www.psoft.hu/termekek/telepules-matrix.html weboldalról lehet letölteni XLS formátumban.
XLS fájl beolvasására bőven van választási lehetőség az R csomagok között: gdata, xlsReadWrite, XLConnect, xlsx, stb. Ezek közül én személy szerint az XLConnect csomagot használom, illetve fogom használni a példa során.
Adatok betöltése:
Az adatok betöltését 2 lépésből oldjuk meg: Az xls fájl betöltése után az adatokat az első munkalapból olvassuk be, ugyanis ez tartalmazza a távolságokat.
|
1 2 3 4 |
library(XLConnect) wb <- loadWorkbook("psoft-telepules-matrix-30000.xls") # A munkafüzet beolvasása data <- readWorksheet(wb, 1) # Az első munkalap betöltése |
Adatok tisztítása:
Az elemzés elvégzéséhez egy numerikus mátrixra van szükségünk, illetve a városok neveire. Amit alakítani kell a jelenlegi adathalmazon:
- Az első oszlopot tartalmazó városnevekből sorneveket csinálunk, majd töröljük.
- Utolsó sorban a psoft promo szövege található, amire értelemszerűen nincs szükségünk.
- Azonos városok távolságánál hiányzó, vagyis (NA) értékek szerepelnek, ezeket le kell cserélni 0-ra.
Megvalósítás:
|
1 2 3 |
rownames(data) <- data[, 1] # Sornév létrehozása data <- data[-nrow(data), -1] # Utolsó sor és első oszlop elhagyása data[is.na(data)] <- 0 # NA értékek lecserélése 0-ra. |
Kész is van a távolságmátrixunk, most már nekieshetünk a többdimenziós skálázásnak. MDS-re több lehetőség is van, én a legegyszerűbbet: a cmdscale függvényt alkalmazom, ami a stat package-en belül található. Paraméterként egy numerikus mátrixot, vagy data.frame-et kell megadni. Alapértelmezetten 2 dimenziót használ, ezt a k paraméterrel lehet állítani. Általában a priori módon határozzák meg.
|
1 |
MDS <- cmdscale(data) |
A koordinátákat az MDS mátrix 2 oszlopa tartalmazza. Ezek alapján szeretnénk kirajzolni a térképet a ggplot2 quickplotja segítségével. Az első oszlop az x koordináta, a második pedig az y.
|
1 2 3 4 |
library(ggplot2) p <- qplot(MDS[, 1], MDS[, 2], label=rownames(data)) p <- p + geom_text() p |
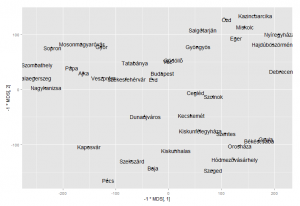
Ezzel a probléma, hogy a tengelyek fel vannak cserélve. Az MDS ugyanis a távolságok alapján nem tudja megállapítani, hogy melyik város van északra, vagy éppen délre. Ha mindkét tengelyre tükrözzük a koordinátákat, akkor már ismerősebb lehet a plot.
|
1 2 3 |
p2 <- qplot(-1*MDS[, 1], -1*MDS[, 2], label=rownames(data)) p2 <- p2 + geom_text() p2 |
Ellenőrzés, a modell jósága:
Az MDS lényege hogy egy adathalmazt dimenziócsökkentéssel könnyebben elemezhetővé tegyen. A dimenziócsökkentési eljárások a legtöbb esetben információveszteséggel járnak. A modell jóságát többféleképpen is ellenőrizhetjük, jelen esetben a determinációs hányados alapján fogunk dönteni.
|
1 2 3 |
library(MASS) shep <- Shepard(data, MDS) summary(lm(shep$yf ~ shep$x))$r.squared |
|
1 |
0.9875959 |
Az információveszteség mértéke kevesebb mint 2% tehát a modell kiemelkedően jónak számít.
Pingback: viagra mail order uk
Pingback: cialis 20 mg price
Pingback: cialis on line
Pingback: how much is cialis
Pingback: cialis price costco
Pingback: Buy brand viagra
Pingback: Buy cheap viagra online us
Pingback: buy albuterol online
Pingback: cheap viagra for sale online
Pingback: cealis
Pingback: cialis professional
Pingback: naltrzone online
Pingback: generic cialis cost
Pingback: cialis over the counter
Pingback: how does viagra work
Pingback: bimatoprost generic best price
Pingback: canadian pharmacy cialis
Pingback: name brand viagra
Pingback: tylenol generic
Pingback: buy chloroquine
Pingback: viagra for sale
Pingback: online pharmacy viagra
Pingback: viagra 50mg
Pingback: best ed pills
Pingback: male ed pills
Pingback: best non prescription ed pills
Pingback: hydroxychloroquine brand name
Pingback: canada online pharmacy
Pingback: pharmacy online
Pingback: Buy cialis
Pingback: Viagra or cialis
Pingback: vardenafil 20mg
Pingback: vardenafil online
Pingback: levitra generic
Pingback: viagra for women judpharmacys
Pingback: wind creek casino online play
Pingback: cialis online purchase
Pingback: golden nugget online casino
Pingback: viagra online prescription
Pingback: real casino online
Pingback: empire casino online
Pingback: generic cialis canada
Pingback: canada pharmacy discounted viagra 100
Pingback: no credit check loans
Pingback: latisse vs generic bimatoprost
Pingback: www.cialis.com
Pingback: personal loan
Pingback: cash loans
Pingback: viagra cost
Pingback: buy viagra in canada
Pingback: Google
Pingback: virgin casino online nj login
Pingback: buy cialis
Pingback: betfair casino online nj
Pingback: cialis 5 mg
Pingback: what is the best usa online casino
Pingback: online gambling sites for us
Pingback: cialis 20
Pingback: Best Online Casinos 2020
Pingback: price check 50mg viagra
Pingback: buy cialis
Pingback: 20 cialis
Pingback: cialis internet
Pingback: buy generic viagra online
Pingback: online casino real money usa
Pingback: buy hydroxychloroquine online
Pingback: online casino usa real money
Pingback: free casino games
Pingback: play online casino real money
Pingback: viagra online
Pingback: sildenafil dosage
Pingback: sildenafil generic
Pingback: brand viagra
Pingback: canadian pharmacy viagra
Pingback: cialis online reviews
Pingback: buy viagra online usa
Pingback: viagra without a doctor prescription
Pingback: tadalafil cialis
Pingback: buy cialis online reddit
Pingback: buy viagra pills
Pingback: levitra
Pingback: canadian online pharmacy cialis
Pingback: free slots
Pingback: online slots for real money
Pingback: http://droga5.net/
Pingback: cialistodo.com
Pingback: viagra without a doctor prescription
Pingback: where to buy viagra online safely
Pingback: buy cheap viagra
Pingback: buy viagra
Pingback: buy cialis brand online
Pingback: buy sildenafil
Pingback: Viagra 120mg for sale
Pingback: Viagra 25 mg without a prescription
Pingback: Viagra 120mg without a doctor prescription
Pingback: sildenafil pills
Pingback: cheapest Viagra 50 mg
Pingback: Cialis 20 mg purchase
Pingback: Cialis 60mg online
Pingback: generic cialis
Pingback: Cialis 10 mg over the counter
Pingback: Cialis 80 mg united kingdom
Pingback: buy viagra generic
Pingback: viagra cheap
Pingback: Cialis 10 mg online
Pingback: Cialis 40mg otc
Pingback: Cialis 40mg purchase
Pingback: sildenafil 200 mg nz
Pingback: order tadalafil 10 mg
Pingback: viagra generic drugs
Pingback: levitra 20mg cost
Pingback: how to buy lasix 40mg
Pingback: furosemide 100mg united states
Pingback: viagra coupons
Pingback: where to buy propecia 1mg
Pingback: canadian online pharmacy no prescription
Pingback: lexapro 10mg for sale
Pingback: where can i buy finasteride 1mg
Pingback: abilify 20 mg canada
Pingback: actos 15 mg pharmacy
Pingback: viagra generique livre sous 48h
Pingback: allopurinol 300 mg australia
Pingback: where can i buy antabuse 500 mg
Pingback: antivert 25mg pharmacy
Pingback: how to buy arava 10mg
Pingback: strattera 10 mg online
Pingback: aricept 10 mg generic
Pingback: sildenafil citrate
Pingback: tamoxifen 10mg purchase
Pingback: cheap cialis
Pingback: ashwagandha 60caps uk
Pingback: atarax 25mg prices
Pingback: augmentin 875/125 mg australia
Pingback: meds without a doctor prescription
Pingback: avodart 0,5mg cheap
Pingback: benicar 20 mg pills
Pingback: buy viagra online
Pingback: sildenafil cost walmart
Pingback: Biaxin 500 mg medication
Pingback: Premarin 0,3mg nz
Pingback: cardizem 90 mg no prescription
Pingback: cialis coupon
Pingback: casodex uk
Pingback: cialis
Pingback: catapres pharmacy
Pingback: ceclor otc
Pingback: ceftin 250mg no prescription
Pingback: generic viagra without a doctor prescription
Pingback: celebrex 100mg purchase
Pingback: celexa australia
Pingback: canadian drugs online
Pingback: cephalexin australia
Pingback: cipro 1000 mg usa
Pingback: cialis without a doctor prescription
Pingback: claritin over the counter
Pingback: viagra
Pingback: slots online
Pingback: rivers casino
Pingback: legitimate online slots for money
Pingback: chumba casino
Pingback: online casino games for real money
Pingback: wind creek casino online play
Pingback: online slots for real money
Pingback: generic viagra
Pingback: pala casino online
Pingback: real money casino online
Pingback: caesars casino online
Pingback: car insurance quotes
Pingback: direct general car insurance quotes
Pingback: auto liability insurance
Pingback: jokes about viagra generic names
Pingback: online car insurance quotes
Pingback: tadalafil
Pingback: abc car insurance
Pingback: car insurance price
Pingback: geico car insurance quotes official site
Pingback: car insurance usaa
Pingback: aaa car insurance quotes reviews
Pingback: erie car insurance quotes
Pingback: ed treatments
Pingback: online personal loans
Pingback: Viagra order
Pingback: payday loans payday loans
Pingback: payday loans delaware
Pingback: best ed pills
Pingback: small installment loans
Pingback: best quick loans
Pingback: online pharmacy viagra
Pingback: short term bad credit loans
Pingback: payday loans no credit check
Pingback: buy amoxil
Pingback: personal loans in nc
Pingback: maker of viagra
Pingback: cbd oil for sale online and reviews
Pingback: cbd oil products
Pingback: cbd oil for sale online and reviews
Pingback: buy sildenafil online uk
Pingback: cbd oil benefits and uses
Pingback: viagra substitutes
Pingback: cbd oil sexual benefits
Pingback: cbd oil for pain dosage
Pingback: payday loans online fast deposit
Pingback: viagra cream price
Pingback: cbd hemp oil benefits
Pingback: sildenafil best price
Pingback: benefits of cbd hemp oil
Pingback: what is the best cbd oil
Pingback: how to write a community service essay
Pingback: viagra mail order
Pingback: uspto assignments database
Pingback: buy an essays
Pingback: scholarship essay writing service
Pingback: essay writing service review
Pingback: term paper writers
Pingback: generic viagra online purchase
Pingback: assignment notebooks
Pingback: essay writing service canada
Pingback: write a college essay
Pingback: university essay writing service
Pingback: canadian viagra 100mg
Pingback: buy cleocin 300mg
Pingback: clomid tablet
Pingback: where can i buy clonidine
Pingback: Canadian generic viagra online
Pingback: clozaril 25 mg over the counter
Pingback: colchicine 0,5mg for sale
Pingback: symbicort inhaler 160/4,5mcg without a doctor prescription
Pingback: Viagra overnight delivery
Pingback: combivent online pharmacy
Pingback: medical school essay help
Pingback: coreg pharmacy
Pingback: compazine 5mg price
Pingback: cialis online
Pingback: coumadin 1mg tablet
Pingback: Pfizer viagra 50 mg online
Pingback: buy cozaar
Pingback: thesis titles
Pingback: https://writemypaperbuyhrd.com
Pingback: how to purchase crestor 10 mg
Pingback: essaywritingservicesjy.com
Pingback: custom essay meister
Pingback: best dissertation services
Pingback: college scholarship essay help
Pingback: cymbalta 20mg pharmacy
Pingback: cheap viagra
Pingback: help writing thesis
Pingback: help with writing research papers
Pingback: dapsone 1000caps nz
Pingback: how to purchase ddavp
Pingback: depakote 250mg without a doctor prescription
Pingback: diamox united kingdom
Pingback: Buy branded viagra
Pingback: differin 15g pharmacy
Pingback: diltiazem without prescription
Pingback: doxycycline 100mg uk
Pingback: viagra prices
Pingback: dramamine 50mg australia
Pingback: elavil 50mg online pharmacy
Pingback: Google
Pingback: where can i buy erythromycin 500 mg
Pingback: etodolac 300mg online pharmacy
Pingback: generic Zithromax
Pingback: cost of flomax
Pingback: flonase nasal spray price
Pingback: garcinia cambogia 100caps usa
Pingback: pumps for ed
Pingback: geodon 80mg over the counter
Pingback: hyzaar 12,5mg united states
Pingback: order imdur 60mg
Pingback: cheap cialis
Pingback: online pharmacy
Pingback: buy cialis online safely
Pingback: buy imitrex
Pingback: how long for cialis to peak
Pingback: how to buy imodium 2 mg
Pingback: how much is viagra
Pingback: check out this site
Pingback: about his
Pingback: cheap viagra
Pingback: buy cialis in canada online
Pingback: imuran purchase
Pingback: indocin 25mg price
Pingback: zithromax order online uk
Pingback: lamisil 250mg cheap
Pingback: levaquin 250mg tablets
Pingback: generic pills
Pingback: cheap lopid 300mg
Pingback: viagra for sale
Pingback: lopressor 25mg no prescription
Pingback: order luvox 100mg
Pingback: macrobid 50 mg online pharmacy
Pingback: meclizine 25mg online pharmacy
Pingback: men's ed pills
Pingback: mestinon 60 mg tablets
Pingback: canadian pharmacies that ship to us
Pingback: micardis without a doctor prescription
Pingback: Floxin
Pingback: cheap antiviral drugs
Pingback: how to buy mobic 7,5mg
Pingback: online pharmacy viagra
Pingback: motrin 400 mg generic
Pingback: mexican online pharmacies
Pingback: nortriptyline 25mg for sale
Pingback: canadian online pharmacies
Pingback: canadian pharmacies shipping to usa
Pingback: non prescription viagra alternative
Pingback: periactin 4mg prices
Pingback: phenergan prices
Pingback: where can i buy plaquenil 200mg
Pingback: prednisolone 10mg cheap
Pingback: prevacid 30mg pharmacy
Pingback: prilosec cost
Pingback: proair inhaler coupon
Pingback: generic viagra online
Pingback: procardia without a doctor prescription
Pingback: buy viagra online
Pingback: order proscar 5mg
Pingback: protonix 20mg online pharmacy
Pingback: provigil 100 mg united states
Pingback: expiry of viagra pills
Pingback: pulmicort without prescription
Pingback: amoxicillin discount coupon
Pingback: cheap pyridium
Pingback: where to buy reglan 10mg
Pingback: doxycycline 100mg
Pingback: remeron pills
Pingback: retin-a cream australia
Pingback: benadryl capsules price
Pingback: revatio price
Pingback: risperdal without a doctor prescription
Pingback: robaxin united states
Pingback: rogaine 5% online pharmacy
Pingback: seroquel canada
Pingback: how to purchase singulair 4mg
Pingback: skelaxin 400 mg medication
Pingback: spiriva canada
Pingback: is viagra over the counter
Pingback: tenormin nz
Pingback: thorazine 50mg united states
Pingback: buy toprol 100mg
Pingback: tricor 200mg medication
Pingback: valtrex no prescription
Pingback: vantin 100 mg united states
Pingback: verapamil no prescription
Pingback: voltaren 100 mg tablet
Pingback: wellbutrin 150mg tablets
Pingback: viagra no prescription
Pingback: zanaflex cost
Pingback: discount cialis
Pingback: zestril medication
Pingback: blog here
Pingback: find out this here
Pingback: buy zocor
Pingback: zithromax buy online no prescription
Pingback: cost of zovirax 400 mg
Pingback: how to purchase zyloprim 100mg
Pingback: zyprexa coupon
Pingback: no precription viagra
Pingback: zyvox 600 mg without prescription
Pingback: sildenafil tablet
Pingback: tadalafil 40mg australia
Pingback: furosemide without a doctor prescription
Pingback: amoxicillin generic
Pingback: escitalopram united states
Pingback: aripiprazole online pharmacy
Pingback: how to buy pioglitazone 15 mg
Pingback: spironolactone cost
Pingback: canadian pharmacy reviews
Pingback: fexofenadine pharmacy
Pingback: glimepiride for sale
Pingback: how to purchase meclizine
Pingback: leflunomide 10mg without a prescription
Pingback: atomoxetine without a prescription
Pingback: cost of donepezil 10 mg
Pingback: anastrozole 1 mg tablet
Pingback: cheap sildenafil
Pingback: irbesartan 150 mg australia
Pingback: dutasteride 0,5 mg coupon
Pingback: olmesartan prices
Pingback: buspirone australia
Pingback: clonidine 0.1mg tablet
Pingback: cefuroxime 125 mg online pharmacy
Pingback: order celecoxib 200 mg
Pingback: cialis online without prescription
Pingback: citalopram 20mg purchase
Pingback: cephalexin without a prescription
Pingback: brand name cialis
Pingback: tadalafil
Pingback: ciprofloxacin canada
Pingback: buy cialis
Pingback: how can i get cheaper cialis
Pingback: where can i buy clindamycin 300 mg
Pingback: clozapine 100mg tablet
Pingback: viagra boners
Pingback: prochlorperazine 5 mg united states
Pingback: brand cialis usa
Pingback: generic viagra without doctor's prescription
Pingback: carvedilolmg generic
Pingback: warfarin over the counter
Pingback: rosuvastatin 10 mg tablets
Pingback: buy desmopressin mcg
Pingback: divalproex 500mg online pharmacy
Pingback: getting viagra in cape town
Pingback: tolterodine price
Pingback: cost of generic sildenafil
Pingback: acetazolamide canada
Pingback: how to buy fluconazole 150 mg
Pingback: what is better viagra or cialis or levitra??
Pingback: how to purchase phenytoin
Pingback: oxybutynin 5 mg coupon
Pingback: doxycycline tablet
Pingback: order bisacodyl 5 mg
Pingback: how to buy viagra tablets in pakistan
Pingback: venlafaxine purchase
Pingback: buy cheap viagra
Pingback: order amitriptyline
Pingback: permethrin 30g united kingdom
Pingback: 141genericExare
Pingback: erythromycin without prescription
Pingback: tadalafil
Pingback: cialis original
Pingback: hlqstwtg
Pingback: estradiol no prescription
Pingback: medication for ed
Pingback: cheap erectile dysfunction pills
Pingback: thtbcswb
Pingback: cost of fluticasone 50mcg
Pingback: alendronate 70mg united kingdom
Pingback: what does female viagra do
Pingback: when is the best time to take cialis
Pingback: nitrofurantoin online pharmacy
Pingback: wat kost cialis
Pingback: hoe kom je aan viagra
Pingback: how ivermectin cause neurotoxicity in dog
Pingback: how much will generic viagra cost
Pingback: after taking zithromax how long till discharge stop
Pingback: where can i buy glipizide 10 mg
Pingback: lasix medication
Pingback: how to buy hydrochlorothiazide
Pingback: buy nitrofurantoin
Pingback: isosorbide 30 mg no prescription
Pingback: order ceftin
Pingback: sumatriptan 100mg coupon
Pingback: cialis farmacie pret
Pingback: loperamide tablet
Pingback: order doxycycline online
Pingback: comprar cialis 10 mg
Pingback: buying cialis online usa
Pingback: why is viagra so expensive
Pingback: how to buy azathioprine
Pingback: canadien cialis
Pingback: propranolol 40mg otc
Pingback: viagra
Pingback: cost of indomethacin 50mg
Pingback: viagra dependency
Pingback: when will cialis go generic
Pingback: top essay writing services uk
Pingback: what should i write my theatre research paper on
Pingback: how do i improve my essay writing skills
Pingback: help me with write my essay
Pingback: why is business ethics important essay
Pingback: lamotrigine otc
Pingback: terbinafine 250mg generic
Pingback: digoxin 0.25mg without a prescription
Pingback: levofloxacin without a doctor prescription
Pingback: medications without a doctor's prescription
Pingback: viagra cost per pill
Pingback: atorvastatin canada
Pingback: amoxicillin 500 price india
Pingback: cost of furosemide 40mg
Pingback: lasix 40 mg cost
Pingback: azithromycin 2018
Pingback: ivermectin 400 mg
Pingback: ivermectin cost
Pingback: ventolin pharmacy uk
Pingback: albuterol 4 mg tablets pharmacy
Pingback: buy generic 100mg viagra online
Pingback: gemfibrozil 300 mg no prescription
Pingback: viagra cost per pill
Pingback: cheap metoprolol
Pingback: can i buy zithromax online
Pingback: clotrimazole 10g nz
Pingback: buying viagra online
Pingback: doxycycline pictures
Pingback: what are prednisolone
Pingback: purchase clomid
Pingback: clomid and estrogen
Pingback: priligy 90mg
Pingback: diflucan in pregnancy
Pingback: diflucan works immediately
Pingback: how to purchase metoclopramide 10 mg
Pingback: synthroid 0.088 mg
Pingback: order ed pills
Pingback: thesisacloud.com
Pingback: how to buy zithromax online
Pingback: phd thesis writing services
Pingback: drug neurontin
Pingback: zithromax buy
Pingback: propecia dht blocker
Pingback: propecia online
Pingback: minocin online
Pingback: united pharmacy india
Pingback: neurontin drug interaction
Pingback: best india pharmacy
Pingback: metformin in pregnancy
Pingback: paxil for children
Pingback: paxil overdose symptoms
Pingback: plaquenil and alcohol
Pingback: levitra pills
Pingback: buying viagra online without prescription
Pingback: generic clomid
Pingback: amoxicillin discount
Pingback: can you buy metformin without a prescription
Pingback: finasteride buy online
Pingback: finasteride
Pingback: cialis without prescriptions canada
Pingback: ed pills that really work
Pingback: lasix 620 mg
Pingback: best pills for ed
Pingback: reputable canadian pharmacy
Pingback: how to buy cialis online uk
Pingback: Zakhar Berkut hd
Pingback: humana online pharmacy
Pingback: 4569987
Pingback: where can i buy cialis without a prescription
Pingback: cialis 5mg tablet
Pingback: how to buy online uk
Pingback: news news news
Pingback: buy 36 hour
Pingback: psy
Pingback: psy2022
Pingback: projectio-freid
Pingback: generic viagra
Pingback: cialis retin a ortho evra patch
Pingback: cash advance payday loan gilroy
Pingback: cute pick up lines for tinder
Pingback: kinoteatrzarya.ru
Pingback: topvideos
Pingback: video
Pingback: viagra erection
Pingback: buy tadalafil0 with pay pal
Pingback: generic lisinopril online
Pingback: afisha-kinoteatrov.ru
Pingback: Ukrainskie-serialy
Pingback: site
Pingback: alternative dating free
Pingback: how does cialis treat bph
Pingback: buy cialis with paypal
Pingback: top
Pingback: ordering cialis online australia
Pingback: which of the following statements about prescription drugs is false?
Pingback: canadian pharmacy no rx
Pingback: cialis cost 20mg
Pingback: buy cialis 36 hour
Pingback: cheap generic cialis
Pingback: cialis online without prescription
Pingback: canada cialis online
Pingback: cure ed
Pingback: cost of valtrex in mexico
Pingback: www pharmacyonline
Pingback: best non prescription ed pills
Pingback: ed help
Pingback: viagra amazon
Pingback: soderzhanki-3-sezon-2021.online
Pingback: chelovek-iz-90-h
Pingback: podolsk-region.ru
Pingback: doxycycline
Pingback: cheap viagra online
Pingback: ed cures that work
Pingback: natural remedies for ed
Pingback: bender na4alo 2021
Pingback: blogery_i_dorogi
Pingback: blogery_i_dorogi 2 blogery_i_dorogi
Pingback: non prescription erection pills
Pingback: buy stromectol pills
Pingback: ivermectin 5
Pingback: dapoxetine with doctor prescription
Pingback: plaquenil 400
Pingback: medicine plaquenil 200 mg
Pingback: ivermectin tablets
Pingback: buy ivermectin nz
Pingback: ed causes and treatment
Pingback: hydroxychloroquine 90
Pingback: ed pharmacy
Pingback: chernaya vodova
Pingback: 66181
Pingback: cheap erectile dysfunction pills
Pingback: Porno
Pingback: vechernyy urgant
Pingback: ukraine
Pingback: viagra online usa
Pingback: viagra from india
Pingback: buy cheap cialis overnight
Pingback: A3ixW7AS
Pingback: hydroxychloroquine oral
Pingback: buy cialis online at lowest price
Pingback: hydroxychloroquine cost 200mg
Pingback: gidonline-ok-google
Pingback: link
Pingback: KremlinTeam
Pingback: medunitsa.ru
Pingback: kremlin-team.ru
Pingback: psychophysics.ru
Pingback: yesmail.ru
Pingback: plaquenil price uk
Pingback: price of cialis at walgreens
Pingback: hydroxychloroquine 200 mg cost
Pingback: Suicide Squad 2
Pingback: psiholog
Pingback: order viagra online in australia
Pingback: sample viagra for free
Pingback: when to take viagra for best results
Pingback: russian pharmacy online usa
Pingback: viagra 100mg price per pill
Pingback: cialis coupon 2019
Pingback: hizhnyak-07-08-2021
Pingback: zithromax 500 tablet
Pingback: importing prescription drugs from canada
Pingback: zithromax 500 mg
Pingback: reager acyclovir
Pingback: regcialist.com
Pingback: online pharmacy no presc
Pingback: viagra after age 70
Pingback: flomax and ivermectil interaction
Pingback: stromectol ivermectin 3 mg
Pingback: ed aids
Pingback: ed medicine
Pingback: plaquenil price canada
Pingback: plaquenil 600 mg
Pingback: humans antiparasitic and stromectol
Pingback: uses of priligy
Pingback: cialis soft tabs canada
Pingback: cheapest generic cialis online
Pingback: prednisone 50 mg price
Pingback: atorvastatin dizziness
Pingback: fluoxetine for dogs reviews
Pingback: zoloft generic side effects
Pingback: quetiapine info
Pingback: plaquenil medicine
Pingback: how does lyrica work
Pingback: most trusted canadian online pharmacies
Pingback: duloxetine and parkinson's disease
Pingback: generic viagra online
Pingback: hydrochlorothiazide and amlodipine
Pingback: how much is ivermectin
Pingback: natural viagra
Pingback: what is lipitor used for
Pingback: viagra cost
Pingback: ospamox deltasone
Pingback: viagra 100mg
Pingback: antiparasitic tablet uses
Pingback: cheap cialis
Pingback: best erectile dysfunction pills
Pingback: ed meds online pharmacy
Pingback: new erectile dysfunction treatment
Pingback: escitalopram and acne
Pingback: where to get cialis online
Pingback: cialis australia
Pingback: buy discount cialis
Pingback: Duna 2021
Pingback: viagra professional
Pingback: sildenafil 50mg
Pingback: lyrica vs cymbalta
Pingback: cialis without prescription
Pingback: viagra prices
Pingback: buying viagra.nz
Pingback: places to buy viagra
Pingback: amoxil price australia
Pingback: an stromectol
Pingback: tadalafil liquid
Pingback: order viagra online
Pingback: clomid 100mg
Pingback: propecia in the us
Pingback: ivermectin lice
Pingback: ivermectin 5 mg
Pingback: ivermectin eye drops
Pingback: viagra
Pingback: eli lilly cialis
Pingback: can you buy prednisone over the counter in greece
Pingback: doxycycline 100mg tablets
Pingback: doxycycline
Pingback: cialis online pharmacy
Pingback: ivermectin tablets dosage
Pingback: viagra script online
Pingback: stromectol and antiparasitic tablets
Pingback: cialis 20 mg best price
Pingback: cialis shop in australia
Pingback: buy cheap viagra online from india
Pingback: best price generic cialis 20mg
Pingback: sildenafil gel
Pingback: ivermectin for humans oral
Pingback: cialis and alcohol symptoms
Pingback: where to buy ivermectin for humans
Pingback: zithramax z-pak prescription
Pingback: cialis france
Pingback: ivermectin for cats fleas
Pingback: best price for sildenafil 100 mg
Pingback: hfa stands for inhaler
Pingback: what is the female viagra called
Pingback: liquid ivermectin
Pingback: viagra alternative naturali
Pingback: cost difference between viagra and cialis
Pingback: the best ed pill
Pingback: cialis tadalafil tablets
Pingback: chemone research tadalafil
Pingback: zithromax tooth infection
Pingback: plaquenil red and yellow capsule
Pingback: viagra best buy website review complaints
Pingback: ed pills online pharmacy
Pingback: generic viagra paypal canada
Pingback: best drugs for ed
Pingback: lisinopril pka value
Pingback: sildenafil coupon
Pingback: fda approved drug ivermectin
Pingback: stromectol pi
Pingback: is dapoxetine approved in australia